Algorithm Solves Longstanding Geometric Challenge

Imagine you are a city planner for a large metropolis, tasked with building two airports. Where should you locate them to ensure everyone can quickly reach an airport to get on a flight? This scenario exemplifies a classic optimization problem in computational geometry known as the Planar Two-Center Problem. In a recent study, NYU Shanghai Assistant Professor of Computer Science Jie Xue and his collaborators have proposed an algorithm to solve this fundamental problem in the fastest way one can expect. This resolves a longstanding open problem in the area of Computational Geometry. Their paper has appeared in the Proceedings of the 40th International Symposium on Computational Geometry (SoCG 2024) in Athens, Greece, this June.

Computational Geometry is a branch of Theoretical Computer Science focused on solving problems related to shapes, points, and other geometric objects using algorithms. The Planar Two-Center Problem involves finding the optimal locations for two congruent circles to cover all points on a map, minimizing the size of the circles. In our airport scenario, the city is the plane with multiple citizens represented as points. The goal is to place two airports (circle centers) so that the maximum distance from a citizen to travel to its nearest airport is minimized.

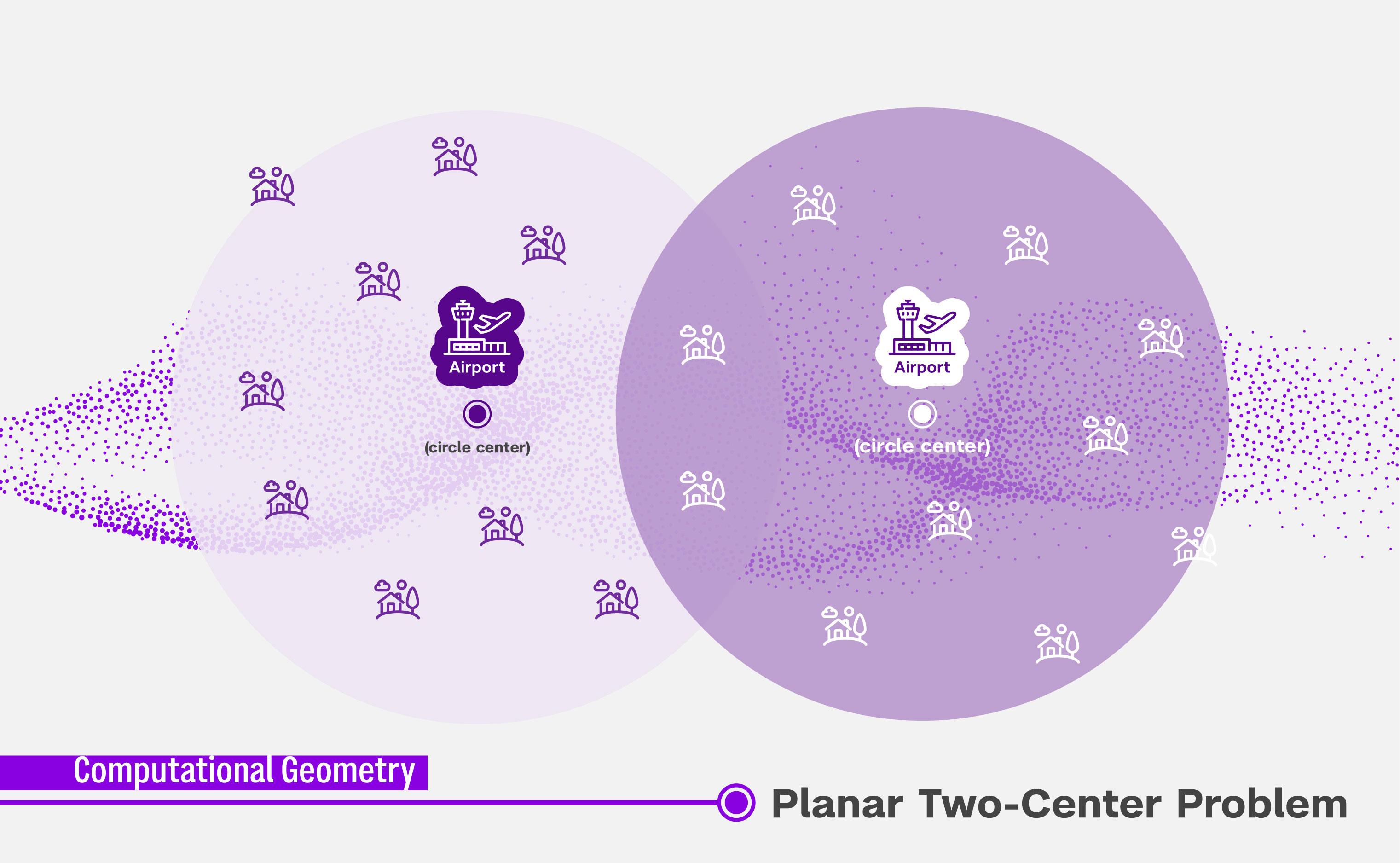
Calculating the solution to this problem is complex and time-consuming. Developing the most efficient algorithm to achieve this in the shortest possible time has eluded scientists for decades. “The Planar Two-Center Problem has been an open question since the 1980s, with a lower bound for the time required to solve it proposed in 1997,” explained Xue. “For nearly three decades, researchers have been working to optimize their algorithms to approach this bound, with limited success.”

In the paper, Xue, along with Kyungjin Cho and Eunjin Oh from Pohang University of Science and Technology, and Haitao Wang from the University of Utah, proposes a new algorithm to solve the Planar Two-Center Problem, significantly improving the previous work. This is the first algorithm whose running time matches the lower bound after decades of research since 1997, making a major breakthrough in Computational Geometry. “Though it sounds highly theoretical, this algorithm has practical applications in city planning and other related real-world problems,” said Xue. “It also has the potential to facilitate exploration of problems involving more than two centers.”

In addition to this paper, four other papers by Xue were accepted by SoCG 2024, making him the only attendee this year with five or more accepted papers. Despite their varied focuses, these papers share the goal of developing efficient algorithms for geometric problems. One paper, titled “An O(nlogn)-Time Approximation Scheme for Geometric Many-to-Many Matching,” won the Best Paper Award of the conference, marking the first time a researcher from mainland China has received this honor. Xue presented two of his accepted papers online at SoCG 2024, engaging with peer researchers who showed great interest in his work.